Eine Studierende lernt an einem Tisch in der Universitätsbibliothek, im Hintergrund sitzen weitere Studierende

Gedankenrundgänge

Eine Person soll in Vertretung einer Firma Kunden in mehreren Orten (A, B, C, . . ., jedenfalls mehr als drei) besuchen. Die Straßenkilometer bzw. Aufwandskosten für die Fahrt von einem Ort zum anderen sind bekannt, ebenso der Ausgangsort. Am Ende der Reise will sie wieder an den Ausgangsort zurück.

In welcher Reihenfolge sollte sie die Orte besuchen, damit sie möglichst wenig Kilometer fahren muss?

Nach einiger Diskussion hat eine Arbeitsgruppe eine Lösung für das Problem entworfen. Hier ist ihr Vorschlag (der Einfachheit halber schreiben wir d(A, B) für die Distanz zwischen zwei Orten A und B):

Beginn: » Ist der Ort x1 der Ausgangspunkt der Reise, so wählen wir als x2, x3 die beiden nähesten Orte zum Ausgangspunkt. Damit können wir bereits eine kleine Rundreise planen: x1 → x2 → x3 → x1. Es gibt nur zwei Rundreisen durch diese drei Orte, nämlich die obige, und die Reise in Gegenrichtung, genauso lang. Daher ist das die kürzeste Rundreise durch diese drei Orte. Diese Route wird noch nicht alle Orte berühren, daher müssen wir sie geeignet erweitern. «

Erweiterung: » Nehmen wir an, wir haben bereits die kürzeste Rundreise x1 → x2 → . . . → xm → x1 durch m Orte gefunden, aber ein Ort y ist von der Rundreise noch nicht erfasst.

Der Ausdruck \(d\left ( x_{i},y \right )+d\left ( y,x_{i+1} \right )-d\left ( x_{i},x_{i+1} \right )\) beschreibt genau den Wert, um den sich die Rundreise durch den Einbau von y zwischen den Stationen xi und xi+1 verlängert. Vergleichen wir also die Größen

$$d\left ( x_{1}, y \right ) + d\left ( y, x_{2} \right )-d\left ( x_{1}, x_{2} \right ),$$

$$d\left ( x_{2}, y \right ) + d\left ( y, x_{3} \right )-d\left ( x_{2}, x_{3} \right ), $$

$$\vdots $$

$$d\left ( x_{m}, y \right ) + d\left ( y, x_{1} \right )-d\left ( x_{m}, x_{1} \right )$$

Dort, wo dieser Wert am kleinsten ist, bauen wir y in die Rundreise ein: x1 → x2 → . . . → xi → y → xi+1 → . . . → xm → x1. Weil die vorherige Rundreise die kürzeste durch die Orte x1, . . . , xm (ohne y) war und y in diese Rundreise an der günstigsten Stelle eingebaut wurde, muss die neue Rundreise die kürzeste durch die Orte x1, . . . , xm, y sein.

Wenn dann alle Orte eingebaut sind, haben wir die kürzeste Rundreise gefunden. Wenn noch Orte fehlen, bauen wir sie nacheinander auf dieselbe Weise in die Rundreise ein, bis alle Orte besucht werden. «

Zwei Studierende besprechen sitzend auf der Universitätsbibliotheks-Treppe Lernunterlagen

Welche ihrer folgenden Überlegungen ist zutreffend?

1. » Das Verfahren ist nicht effizient, denn es hat ja keinen Sinn, den Vertreter erst durch drei Orte zu schicken, und im nächsten Schritt wieder durch dieselben drei Orte und einen vierten, usw. . . . «

2. » Das Verfahren geht im Kreis und kann nicht funktionieren, weil am Beginn jedes Erweiterungsschrittes bereits die kürzeste Rundreise gebraucht würde. «

3. » Das Verfahren enthält einen Trugschluss und muss nicht die kürzeste Rundreise ergeben. Der Einbauschritt sucht nicht unter allen möglichen Rundreisen durch x1, . . . , xm, y die kürzeste aus, sondern vergleicht nur einen Teil der möglichen Rundreisen. Es ist daher nicht sicher, dass die kürzeste von allen Rundreisen innerhalb des Verfahrens überhaupt in Erwägung gezogen wird. «

Überlegung 1 trifft den Sinn des Verfahrens nicht. Denn dort wird zuerst schrittweise berechnet, wie die Rundreise zu planen ist, und erst wenn die Planung fertig ist, soll der Vertreter ausgeschickt werden.

Überlegung 3 lässt sich leicht entkräften. Das Verfahren beginnt mit einer Rundreise der Länge drei, die leicht zu finden ist. Der erste Erweiterungsschritt macht daraus eine Rundreise der Länge 4 und so weiter, bis die Rundreise durch alle Orte geht. Das Verfahren geht also nicht im Kreis, sondern jeder Schritt verlängert die Reise.

Überlegung 3 trifft zu, wie man mit einem Gegenbeispiel wie unten angegeben zeigen kann.

Es hilft womöglich dem Verständnis ...

... wenn man folgendes Beispiel betrachtet. Seien mit A, B, C, D, E fünf Orte gegeben und sei bereits die kürzere Rundreise A → B → C → D → A gegeben. Der Ort E sei nun von B und D sehr weit entfernt, oder es herrsche stets Stau, wodurch die Kosten dieser Strecke immens werden. Da bei jedem Einbau von E einer der Orte B, D beteiligt ist, ergeben sich sehr große Gesamtkosten.

Wählt man jedoch etwa die Route A → E → C → D → B → A, vermeidet man diese sehr aufwendigen Strecken und kann wesentlich geringere Gesamtkosten erhalten, selbst wenn alle Kosten der verwendeten Teilstrecken zwischen den ersten vier Orten A, . . . , D etwas größer werden.

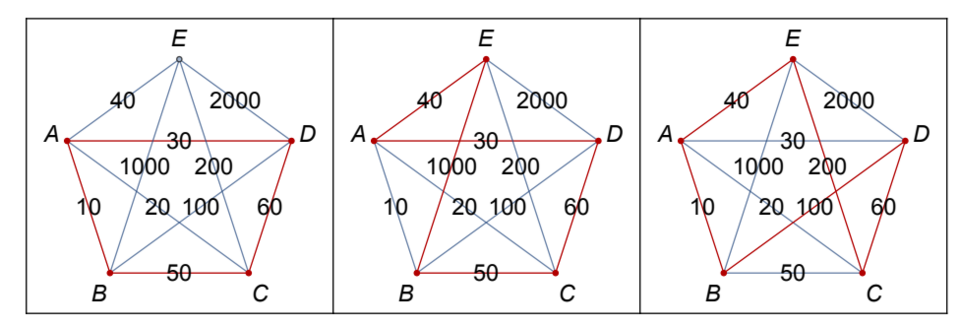
In den Diagrammen in der Abbildung wird das Beispiel noch einmal konkret mit Zahlenwerten dargestellt. Die Kosten der zweiten Runde des Verfahrens durch vier Orte sind 150, nach dem nächsten Erweiterungsschritt springen sie auf 1180 an. Die günstigste Route kommt jedoch auf nur 410, fast ein Drittel.

Zurück
Weiter