Eine Studierende und ein Studierender lernen gemeinsam an einem Tisch in einem Lernraum der Universitätsbibliothek Graz.

Qualitative Information ausnutzen

Gegeben sei eine Funktion \(f:ℝ \rightarrow ℝ \) mit den folgenden zwei Eigenschaften:

f(x) > 0 für alle x
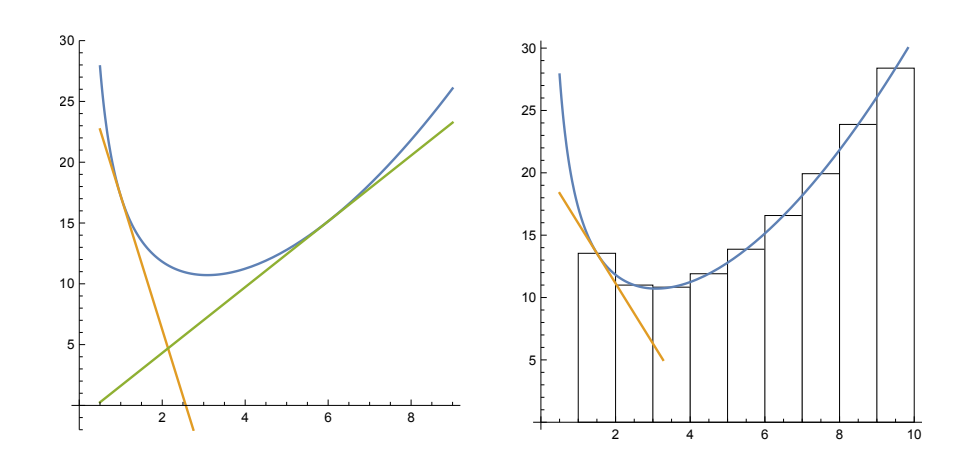
Durch jeden Punkt auf der Kurve von f kann man eine Gerade zeichnen, die zur Gänze unterhalb der Kurve verläuft. (Siehe Skizze unten.) – Funktionen mit dieser Eigenschaft nennt man auch konvex.

Wir wollen die Fläche zwischen der x-Achse und der Kurve von f im Bereich von x = 0 bis x = 10 zumindest näherungsweise berechnen. Dazu teilen wir das Intervall [0, 10] in kleine Teilintervalle auf, und über jedem Teilintervall errichten wir ein Rechteck, dessen Höhe genau der Wert der Funktion am Intervallmittelpunkt ist. Zum Beispiel ist die Höhe des letzten Rechtecks in der Skizze f(9.5). Wenn wir die Flächen dieser Rechtecke summieren, erhalten wir eine Näherungsformel für die Fläche unter der Kurve.

Obwohl diese Aufgabe an der Tür zur Integral- und Differentialrechnung steht, lässt sie sich mit Anschauung ohne höhere Mathematik lösen! Als Hilfestellung haben wir in einem der Rechtecke eine Tangente an die Kurve von f gezeichnet.

Es gilt die erste Antwort: Die Gesamtfläche unter den Rechtecken ist nicht größer als die Fläche unter der Kurve. Wir betrachten ein einzelnes der Intervalle aus der Näherungskonstruktion, mit dem eingezeichneten Rechteck und dem Kurvenstück. Wenn x der Mittelpunkt des Intervalls ist, dann ist laut Konstruktion f(x) die Höhe des Rechtecks. Durch den Punkt (x, f(x)) geht eine Gerade, die zur Gänze unter der Kurve von f verläuft. Diese Gerade haben wir in der Grafik unten eingezeichnet und einige Punkte in der Zeichnung benannt.

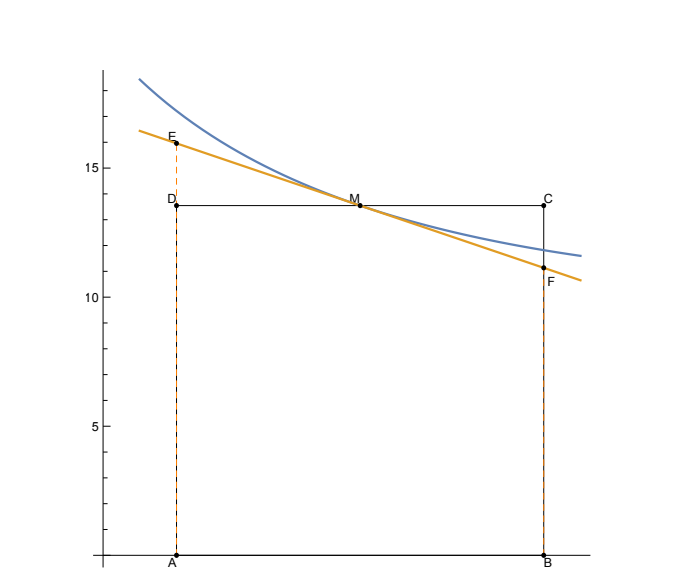
Du kannst es der Abbildung entnehmen: Die Seiten DM und MC sind gleich lang, daher sind die Flächen der Dreiecke MDE und MCF gleich. Also hat das Rechteck ABCD die gleiche Fläche wie das Viereck ABFE.

Dieses Viereck liegt aber zur Gänze unter der Kurve. Daher kann die Fläche von jedem der Rechtecke in der Näherungskonstruktion nicht größer sein als die Fläche des Kurvenstücks über dem entsprechenden Intervall. Wenn man nun die Fläche aller Rechtecke zusammenzählt, erhält man keine größere Fläche als die Fläche unter der Kurve.